Table of Contents
<texit info> author=Johnny Rieper, Bent Bisballe Nyeng and Kasper Sohn title=Marvin - The Balancing Robot. </texit>
Lab Report 1 - Gyroscope Communication
Date: January 2nd 2009
Duration of activity: 8-14
Participants: Kasper, Bent and Johnny
Goal
Make Marvin able to communicate with gyroscope.
Plan
- Build the robot in LEGO following the instructions on the mathworks website1).
- Make a test program to test if the gyroscope is working.
- Find or create a class for the gyroscope communication.
Theory
Analogue to Digital Conversion and Limitations
The main problem when dealing with sensors is that the real world is continuous and when we want to interpret these data it has to be digitized (discretized) in some way. This is done with an analogue to digital converter (A/D-converter or simply ADC). The opposite applies when we have a digital value, such as an integer and this is converted to an analogue value (D/A-converter or DAC). This in itself is a huge area, and the conversion itself will not be covered further. The important thing to remember is that in order to get an appropriate estimate of the real world the samples that you take from your sensor has to be taken often enough so that you will not loose vital data. How often one should sample depends on the application, but as a rule of thumb one should sample minimum twice as fast as the highest rate of different that will occur. As an example, if you want to reproduce a sinus with the frequency of 100 Hz, you will have to sample with 200 Hz. A higher sample rate will produce a more accurate output, but will also need more computational power. The gyroscope utilizes the ADC so that it is possible to get readings from the gyroscope.
Gyroscope
The gyroscope used has been purchased from HiTechnic 2) and is shown on the picture below. The housing is a standard Lego Mindstorm sensor so it fits with other sensors, and is more easily incorporated in a building scheme which purely uses LEGO bricks.
The gyroscope is produced to work seamless with the LEGO NXT Brick. It connects to the NXT using a standard wire and utilizes the analogue interface. The gyroscope contains a single axis gyroscopic sensor that detects rotation and returns a value representing the number of degrees per second of rotation. The gyroscope sensor measures up to +/- 360 degrees per second of rotation and these readings will be signed if the correct offset is used.
As not all gyroscopes are identical there will be some minor differences in the offset, but the manual that came along with the gyroscope, indicates this to be around 620. This is the offset value has to be subtracted from the readings from the gyroscope in order to get a signed reading.
The sensor can be read 300 times per second (an interval of 3.33 times per second), which correspond to a sample rate of 300 Hz.
The gyroscope operates in relative values, which means that it can not tell where e.g. upright is. One have to “show” where that is, and from there the gyroscope readings will show how fast the gyroscope is moving from that position. To get an accurate reading it might be necessary to read the value from the right position over some time (e.g. 2 seconds) and from that generate a mean value. This mean value of offset can then be used in further calculations to increase accuracy.
The axis of measurement is in the vertical plane with the gyroscope sensor positioned with the black end cap facing upwards, as illustrated in thye figure below.
The correct placement of the gyroscope can be seen in the building instructions
Building the Robot
Preliminary considerations
Our primary goal is to make a balancing robot, and therefore it would be nice to eliminate the possibility of failure due to a bad build. This is the reason why we chose to re-use the instructions provided as seen in the building manual3). We know that this design is working. Another reason for choosing this design is that there exists extensive simulation material on this specific robot, which might make it easier to fine-tune the parameters later on.
The Build
The build is pretty straight forward, as the building instructions is well written and also accompanied by photos. One thing to note though, is that the robot is fairly symmetric, so building instructions is only provided for one side of the robot and it is up to the builder to mirror the other side. This is however no problem because of the good photos.
The finished robot can be seen in the picture below.
One thing worth noting is that the ultrasonic sensor is shifted slightly to the left. This is because it is important that the gyroscopes fix point is centered on the vertical axis of the robot. Positioning of the gyroscope is well documented in the building instructions. Below is a photo of the gyroscope in place.
Peripheral Connections
| Sensor | Output | Unit | Data Type | Maximum Sample [1/sec] | Port |
|---|---|---|---|---|---|
| Rotary Encoder Left * | angle | deg | int32 | 1000 | B |
| Rotary Encoder Right * | angle | deg | int32 | 1000 | C |
| Ultrasonic Sensor | distance | cm | int32 | 50 (N1) | 2 |
| Gyroscope Sensor | angular speed | deg/sec | uint16 | 300 | 4 |
| Actuator | Input | Unit | Data Type | Maximum Sample [1/sec] | Port |
|---|---|---|---|---|---|
| DC Motor Left * | PWM | % | int8 | 500 | B |
| DC Motor Right * | PWM | % | int8 | 500 | C |
*The rotary encoders and DC Motors (left and right respectively) utilizes the same port.
Pros and Cons About the Design
As mentioned earlier, this is a well documented and working design. This is of great importance, because we can eliminate this as a factor of error later on. Another issue that have proven important in our experiments is the ability to easily remove the battery for recharging. This may not seem important at this point, but the characteristics of the voltage applied to the motors vary greatly with the charge level of the battery, and therefore the behaviour of the motors varies. It is therefore a nice feature that the battery is easy to remove without tearing the robot apart.
In the group we discussed what effect the wheel diameter will have on the robot. Wheels with a larger diameter will travel a longer than smaller wheels for the same amount of power applied to the motor on which the wheel is mounted. We decided that the resolution of the wheel rotational properties were accurate enough to go with the larger wheels, and these wheels were also used in the design we used in the first place, and therefore was a well-proven design.
A thing worth mentioning is the construction of the wheel mounting point and wheelbase which can be seen on the picture below
This construction provides a rigid frame that will prevent structural wobbling. This is important because of the sudden movements forward and backward motions a balancing robot evidently will make.
The wheel mounting point is cleverly made so that there will be no loss of power between the motor and the wheel. We used the standard wheels throughout testing, but found these to have to much friction when driven on rugged carpet. Although they have a cleverly designed mounting point we found that this was not necessary in our implementation and opted to go with the wheels shown below.
Implementation
Numerical Readings from the Gyroscope
A gyroscope measures degrees per second or simply angle velocity and therefore we must use numerical integration in order to get the angle. A gyroscope has a bias which is simply an offset and naturally we want to eliminate this offset by calibration methods at the beginning of the program. If we do not calibrate, the integration, e.g. a running sum, will add the offset contribution for every sample and diverge resulting in an unstable system. If we calibrate the integral, this problem will be reduced, but unfortunately the bias of the gyroscope tends to drift and therefore one needs to recalibrate if possible or find other heuristic methods in order to avoid an escalation of the error. Sensor fusion is suggested, which rely on the somewhat complex implementation of the Kalman filter, which may combine sensor inputs an re-estimate the most likely bias value while offering an indication of how much trust we may put in this value. A sensor fusion could be used to combine an accelerometer or inclinometer with the gyroscope, but it seems a bit ambitious to implement a Kalman solution given the scope of this project - also keeping in mind that there are many other areas of improvement that should be evaluated first.
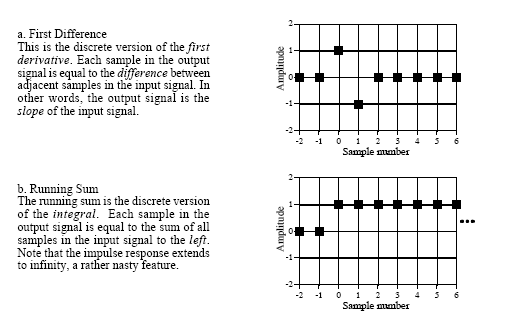
In order to do a discrete integration we simply need to look at a simple recursive difference equation, which in this case will be a running sum. Recall the difference equations for simple first order derivatives and a very simple integration:
Integration: <latex>y_n=x_n+y_{n-1}</latex><texit>$y_n=x_n+y_{n-1}$</texit>
First difference: <latex>y_n=x_n+x_{n-1}</latex><texit>$y_n=x_n+x_{n-1}$</texit>
Each sample in the output signal is a sum of weighted samples from the input. The reason for pointing out the first order derivative as well is that they (of course) are closely related which becomes clear in the illustration below. 4)
There are many types of algorithms for numerical integrations that are far more advanced and all of them or based on some kind of interpolation technique, but for now we will rely on the simplest form which is the running sum.
Programming
LeJOS has its own GyroSensor class5). But apparently it only supports reading of the raw gyroscope values, and offers no interpretations (it is essentially just a wrapper of the SensorPort class, with an offset). We therefore programmed our own GyroscopeSensor class, with methods for reading out both the angle velocity, and the calculated (integrated angle velocity over time) angle.
This class wraps the gyroscope sensor, and offers readouts as either angle velocities, or as integrated angle velocities over time (angles).
The angle velocities can be read raw from the sensor port, but must be subtracted with an offset defining the stand-still gyroscope. This value is according to the documentation approximately 620, but may vary from gyroscope to gyroscope. We made some experiments and found the value 595.5 to be pretty accurate.
This value is however not accurate enough when run over a large quantity of time, which will make the integration drift, thereby making Marvin unable to keep its balance.
The solution was to use the measured value as an initial value, and then use a weighted average of all measured angles over time, where the last measured angle is weighted very low. We tested the solution with a variety of values, and found the value 0.999999 to be pretty good (one might think the having a static 595.5 might do the same, but experiments show otherwise).
These constants are hard coded into the program with the following names and values:
| Variable | Value |
|---|---|
| lastOffset | 595.5 |
| a | 0.999999 |
For the integration over time algorithm we use a simple sum multiplied by the delta time since last call. This delta time is acquired by calling the System.currentTimeMillis() method, which reports the number of milliseconds since the NXT was been turned on.
In the following excerpt from the GyroscopeSensor class can be seen the weighted average algorithm in the getAngleVelocity() method, and the integration over time algorithm in then getAngle() method.
public class GyroscopeSensor { private SensorPort port; . . . private double getAngleOffset() { double offset = lastOffset * a + (1.0 - a) * (double)port.readValue(); lastOffset = offset; return offset; } . . . public double getAngle() { int now = (int)System.currentTimeMillis(); int delta_t = now - lastGetAngleTime; // Make sure we only add to the sum when there has actually // been a previous call (delta_t == now if its the first call). if(delta_t != now) { angle += getAngleVelocity() * ((double)delta_t / 1000.0); } lastGetAngleTime = now; return angle; } }
The full source code for this class can be found in the file GyroscopeSensor.java in the Marvin code tarball 6)